どうやって測る？～星や銀河の距離：astronomy010

遠い距離を測る方法とは？

事務・受付担当の「さいたまあちゃん」です。

 

前回は、「元素の由来」ついて解説しました。

今回は、「星や銀河までの距離をどうやって測るのか？」について解説していこうと思います。

 

今まで解説してきたように宇宙はとてつもなく広く、一番近い恒星でも光の速さで4年以上かかる距離ですが、これについて、

「人類が現在の技術で到達できないこの距離をどうやって計測するのか？」

こんな疑問が沸きませんか？

 

実は宇宙というスケールまで行かなくとも、地上での測量技術がヒントになります。

それは「三角測量」です。

なるほど・・と思える、究極の業！

また疑問が沸くと思いますが、三角測量を使うとして、離れた2地点で測る必要があるため、「そんな遠い距離をどうやって移動する？」

ですが、私達は乗っているじゃないですか！　地球という乗り物に。

 

具体的には、半年の期間をおけば同じ地球上で観測しても、地球は太陽の周りを1年で公転しているので、ちょうど反対側へ移動できます。

この2つの位置での星の見える角度を計算できる三角形をつくれば、辺の長さ＝星までの距離を測ることが出来ます。

 

この測定方法を「年周視差」と言います。

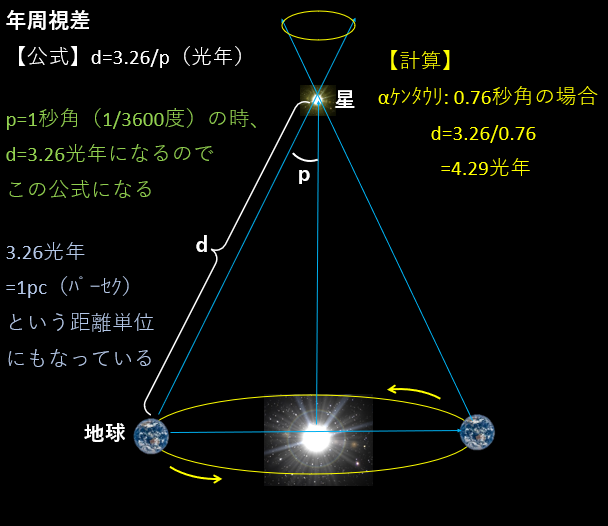
それでも、限界はあり！

測りたい星が遠くにあるほど、角度は小さくなります。　三角形の頂点が鋭角になっていくからです。

したがって、現在の技術では3000光年までが限界とされています。

 

それでも、1辺が3000光年で、もう一辺が太陽までの距離の1倍＝約0.000016光年なので、1.9億：1の比率の細長～い三角形を作って計測する事が必要なので、驚異的な高精度が求められます。

 

それが今の技術では1割の誤差で計測可能なのですが、約3000光年くらいまでという限界があります。

それより遠いと、計測不能であるか誤差が無視できなくなります。

宇宙の距離はしご

では、3000光年より遠い場所は計測不能なのか？　となりますが、人間は賢いです。

別の計測方法を考え付きました。

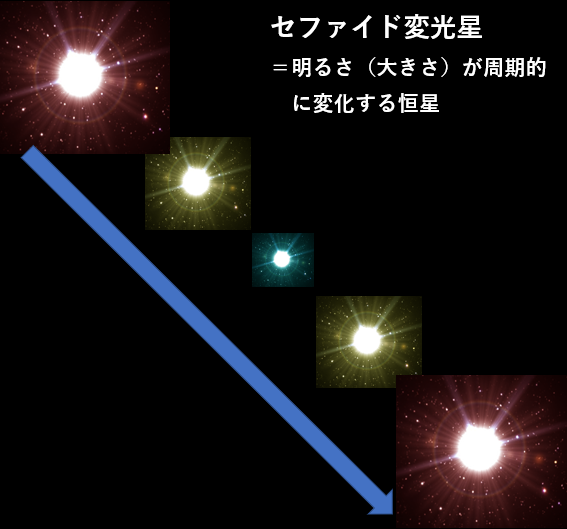
それは「セファイド変光星」という種類の星を指標にする方法です。

セファイド変光星とは、数時間～約100日までの一定の周期で明るさを変える恒星であり、最大光度は周期の0.9乗に比例するという規則性を発見しました。

星の実際の明るさが分かれば距離がわかります。

 

例えるなら、太陽がどんなに明るくとも遠くから見れば小さな星に見えますので、数ｍ先にある小さなLEDと同じ明るさに見えるかもしれません。＝見かけの明るさという

しかし、目の前にある時の明るさ（＝実際の明るさという）が分かれば、どれほど離れていればその「見かけの明るさ」となるかが計算できるからです。

 

その規則性を見つけるには、先ほどの測定方法の限界である3000光年以内にある変光星を調べれば、裏付けられます。（一番近いセファイド変光星は、431光年にあるあの「北極星」です）

ただし、セファイド変光星以外の恒星は距離を測れない事にはなります。⇒それでも銀河系外にある銀河の距離を測るときには、その銀河内に1つでもセファイド変光星を見つければその銀河までの距離がわかることを意味します。

 

つまり、計測方法を変えながら、まるではしご（梯子）のようにつぎ足しながら、計測していくので「宇宙の距離はしご」と呼んでいます。

当然、セファイド変光星を使った方法にも、6500万光年くらいまでという限界があり、また更に別の梯子＝計測方法へとつないでいきます。

 

「次のはしごがあれば、その前のはしごは不要では？」と思うかもしれませんが、各はしごには長さが決まっている＝つまり、

短い距離方向の測定も限界がそれぞれあるので、各距離はしごは必要なのです。

次のはしごとは、あの・・・

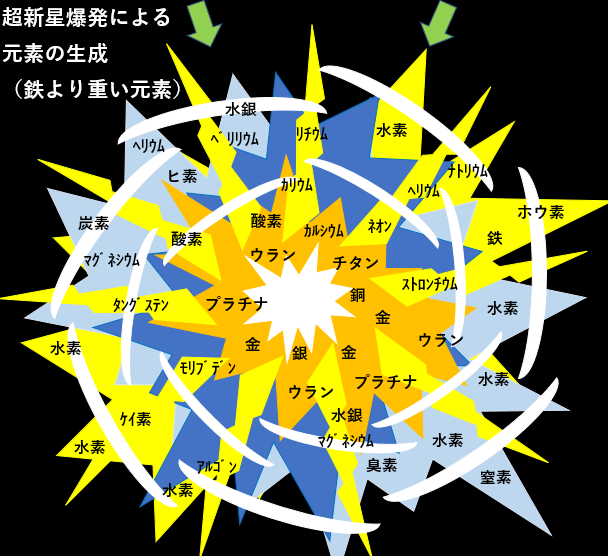
以前少し触れましたが、Ⅰa型超新星を使います。

Ⅰa型超新星（太陽の8倍以下の質量の恒星が寿命を迎えて白色矮星になった後、近くの恒星のガスを吸って爆発する現象）

も、距離と実際の光度の規則性があることが、その前の距離はしご（セファイド変光星）からわかっていて、指標となります。

この場合もセファイド変光星と同様、距離を測りたい銀河の中に1つでもⅠa型超新星を見つけることが出来れば測ることが出来ます。

 

この方法にも、数十億光年くらいまでという限界があります。

最後の距離はしご

最後の距離はしごは、「ハッブル-ルメートルの法則」を使います。

今から100年位前に、ハッブルという天文学者が大発見をしました。

 

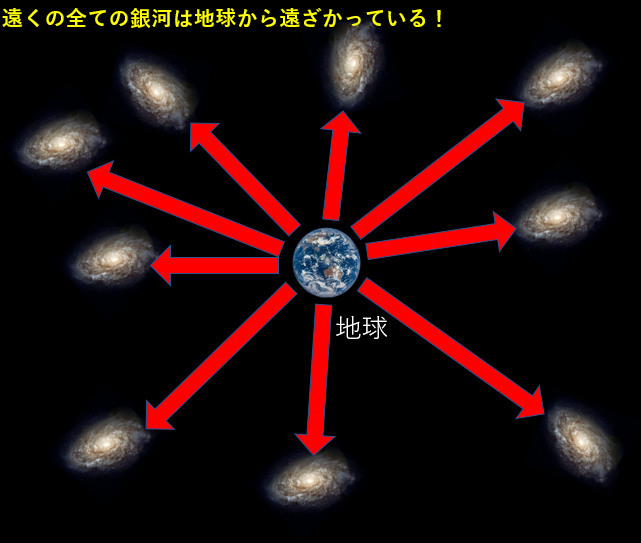
遠くにあるすべての銀河は、地球から距離に比例して速く遠ざかっているという事です。

つまり、距離が2倍になれば速度も2倍に、距離が3倍になれば速度も3倍になるという意味です。

 

「そもそも、銀河が遠ざかる速さってどうやって測るの？」という疑問がまた新たに沸きます。

それは「赤方偏移」という現象で、救急車が遠ざかるときに音色が変わるように、光も波長が長く変化します。

これを「光のドップラー効果」と言います。

 

具体的には、赤方偏移から銀河が遠ざかる速さがわかり、速さがわかると、ハッブル－ルメートルの法則により、

距離がわかるというものです。

この規則性の裏付けも、前の登場した距離はしご（Ⅰa型超新星）で検証しているのです。

このように、4つのはしご（計測方法）を紹介してきましたが、一番精度が高いのは1番最初のはしごである

「年周視差」です。

他のはしごである計測方法は、年周視差に比べて誤差が大きくなっていく傾向にあります。

と同時に、最初のはしごである年周視差の精度を上げることにより、その後に続く距離はしごの精度が向上します。

 

将来的には、精度の高い人工衛星を飛ばして、年周視差の3000光年の測定限界を10倍まで拡張させる計画があるようです。

なぜ、銀河は遠ざかる？

この発見が「宇宙は膨張しているのだ」という「ビッグバン理論」に結び付きます。

次回はここを詳しく解説していきます。