童話と相対性理論：astronomy017

SF版浦島太郎

事務・受付担当の「さいたまあちゃん」です。

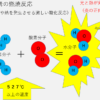
前回は、「速く動くものは時間が遅く流れる」について、特殊相対性理論を使って解説しました。

今回は、それを式で解説したいと思います。

有名な童話の中に「浦島太郎」というのがあります。

太郎は3年間竜宮城で過ごし、故郷に戻ると地上ではなんと700年もの年月が経過していて、知人は誰もいませんでした。

3年で700年も経過するという事は実際にあり得るのでしょうか？

このお話をSF版にアレンジしてみます。

むかしむかし、浦島太郎という25歳くらいの男性がいました。

ある日の事、太郎は海岸に行くと亀に似た大きな円盤があり、子供が石を投げてぶつけていました。

太郎は石を投げるのを止めさせると、

その中から美しい女性が現れ「ありがとうございます。　お礼をしたいので一緒に来ませんか？」と誘われ、

その亀のような乗り物に乗り込みました。

女性はこの乗り物を「竜宮城」と呼んでいて、その中では太郎は色々とおもてなしを受けました。

居心地が大変良かったのであっという間に3年の月日が流れました。

「竜宮城」はその間宇宙を飛び、往復700光年の距離を光速に近い速度で移動していました。

浦島太郎が地球へ戻ると700年の年月が経過していました。

というお話になります。

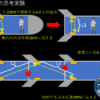
宇宙船などが光の速度に近づくほど特殊相対性理論の効果により、船内の時間がゆっくりと進みます。

（例）光速の90％の速さで宇宙船が1年飛ぶと、地球は2.3年経過する

t=地球時間(年)、T＝宇宙船時間(年)、V＝宇宙船の相対速度は光速の何(％）、C＝光速＝100(％)とすると、

【速度による時間の遅れの式】　t=T/√(1-(V^2/100^2))・・・この式に代入　(/=÷、√=ルート、^2=2乗)

t＝1/√(1-(90^2/100^2))≒2.3年

となるからです。

【考察】浦島太郎が3年で700年経過したというのは、

t＝3/√(1-(99.99909^2/100^2))≒703.2年・・・このように光速の99.99909％の速さで宇宙船が3年飛ぶと、地球は703.2年経過します。

（ただし加減速は1Gで光速近くまで加速するのに1年かかるが、この例では未知の技術で一瞬で安全に出来ると仮定）

↓縦軸に地球時間、横軸に宇宙船の速さとするグラフにするとこのようになります。　(宇宙船内の経過時間はどの速度でも1年として計算)

比例グラフではないところがポイントです。

地球時間は宇宙船の速度が光速の70～80％を超えた以降に大きく遅れ出し、小数点以下9が増える毎に大きくなります。

したがって、日常私達が体感できる低速度では、速度による時間の遅れはほとんど体感できない事になります。

不思議ですね！

それでも、ある程度長い時間をかければ、例えば一生（100年間）では約40分も地球時間は遅れます。

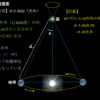
その理由は、地球は太陽の周りを1年でまわっていて(秒速29.8km)、太陽系を含む銀河は2億年で1回転をしていて(秒速230km)、銀河系全体はうみへび座方向へ移動している(秒速600km)からです。

これらを相殺すると地球は秒速370kmで移動していることになり、これは光速の約0.123419％であるからこれを先ほどの数式に当てはめて計算すると、

t＝100/√(1-(0.123419^2/100^2))≒100.0000762年≒100年と40分　（ただし、この場合地球が基準の「t」でなく移動する乗り物とみなすので、t＝銀河系の外の時間で、T=地球時間となる）

言い換えると、私たちは地球という乗り物に乗っているおかげで、一生で40分だけ未来へ進む事になります。

さらに言い換えると、一生で40分も老化を抑えているとも言えます。

700年は経過しませんが、私達も浦島太郎と似たような体験をしていることになります。（全人類がそうなるので何も変化は感じませんが）

これは、最近リメイクされた「猿の惑星」という映画でも同じ理屈です。

次回は、特殊相対性理論についてさらに別の解説をしたいと思います。

では、また。